LICZBY
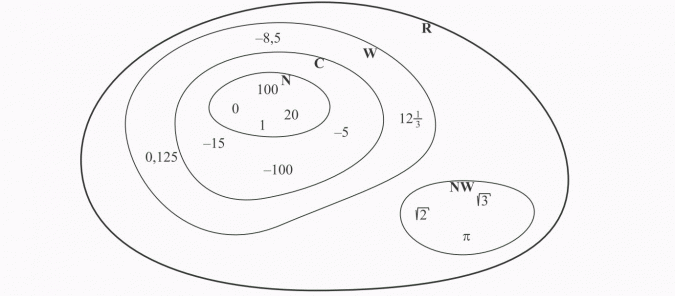
Zbiory liczb
Każdą liczbę naturalną, czyli ≥ 0 i bez liczb po przecinku oznaczamy jako "n".
Wszystkie liczby, które nie mają liczb po przecinku, czyli liczby całkowite, oznaczamy jako "c".
Liczby wymierne, czyli te, które można przedstawić za pomocą dodatniego ułamka oznaczamy jako "w".
A te których nie można, to liczby niewymierne, oznaczamy jako "nw".
Wszystkie liczby jakie mamy to liczby rzeczywiste. Oznaczmy je jako "R".
Ułamki
W matematyce wyróżniamy 2 typy zapisu ułamków:
- ułamki zwykłe
- ułamki dziesiętne.
W ułamku zwykłym na "górze" jest licznik, a na "dole" mianownik.
Żeby dodać ułamki zwykłe oba muszą mieć te same mianowniki.
W tym celu jest skracanie i rozszerzanie ułamków.
Skracanie ułamków: Kiedy mamy mianowniki 32 i 16 nie możemy ich dodać. Ale jeśli mianownik i licznik mają wspólny dzielnik to można je skrócić, dzieląc mianownik i licznik przez tę samą liczbę.
Rozszerzanie ułamków: to odwrotność skracania. Licznik i mianownik mnożymy przez tę samą liczbę.
Przy mnożeniu i dzieleniu ułamków nie sprowadzamy ułamków do wspólnego mianownika. Mnożymy przez siebie licznik i mianownik, np. 1/3x4/5=4/15; 2/5x5/7=10/35=2/7. Dzielenie to natomiast mnożenie przez odwrotność ułamka. Odwrotność - ułamek "na odwrót" np. 3/5-5/3.
Ułamki dziesiętne to tak właściwie ułamki zwykłe o mianowniku: 10,100,1000,10000 itd. Dlatego możemy je dodawać i odejmować jak ułamki zwykłe:
Tzn.: 0,01=1/100; 0,303=303/1000
Np.: 0,303+0,01=303/1000+10/1000=313/1000 0,303-0,01=303/1000-10/1000=293/1000
Oczywiście nie zawsze taki sposób jest szybki, dlatego możemy rozszerzać i skracać ułamki dziesiętne.
Rozszerzamy do wspólnego mianownika dopisując zero (zera) na koniec ułamka, a skracamy zabierając zero (zera) z końca.
Ułamki dziesiętne mnożymy jak zwykłe liczby i przesuwamy przecinek o ilość miejsc po przecinku obu liczb w lewo albo mnożone liczby zmieniamy na ułamki zwykłe.
Przy dzieleniu ułamków dziesiętnych przesuwamy przecinek w dzielniku i dzielnej o tyle pól, żeby dzielnik był liczbą całkowitą. Np.: 2:0,5=2,0:0,5=20:5=4
Każda liczba ma odwrotność i przeciwność (odwrotności używamy do m.in. dzielenia ułamków) Odwrotności to liczby, w których zamieniono ze sobą licznik i mianownik. Przeciwność to ta sama liczba, ale ze zmienionym znakiem: plus na minus i minus na plus.
Przykłady: liczba=17 przeciwność=-17 odwrotność=1/17 liczba=xa przeciwność=-x odwrotność=1/x
Wartość bezwzględna
Wartości bezwzględne dzięki którym określamy jak daleko od 0 jest dana liczba. Jest to odległość na osi liczbowej. Zapisujemy tą wartość w nawiasie [ ]. Np. 8=[8] -9=[9]. Używa się też tego do zapisywania odległości od x'a, np. [5]=3-x
Podzielności liczb
Liczby nie dzielą się przez 0.
Każda liczba jest podzielna przez 1.
Liczby parzyste są podzielne przez 2.
Liczba dzieli się przez 3 jeśli suma jej cyfry jest podzielna przez 3, np. 345, 3+4+5=12.
Liczba jest podzielna przez 4 jeśli jej 2 ostatnie cyfry są podzielne przez 4, np. 4980.
Liczba jest podzielna przez 5 jeśli jej ostatnia cyfra to 0 lub 5, np. 5797865.
Liczba jest podzielna przez 6 jeśli dzieli się przez 3 i 2 (3x2=6, tę zasadę często się stosuje), np. 534.
Liczba podzielna jest przez 9 jeśli suma jej cyfr dzieli się przez 9.
Liczba dzieli się przez 10 jeśli jej ostatnia cyfra to 0.
Liczba dzieli się przez 25 jeśli jest dwie ostatnie cyfry to 00,25,50 lub 75
Liczba dzieli się przez 50 jeśli jej dwie ostatnie cyfry to 50 lub 00.
Liczba dzieli się przez 100 jeśli jej 2 ostatnie cyfry to zera.
Zaokrąglenia
Liczby zaokrąglamy:
- w dół, jeśli ostatnia cyfra to 4 lub mniejsza;
- w górę, jeśli ostatnia cyfra to 5 lub większa,
Np. 3,5≈4 ; 3,45≈3,5
WAŻNE JEST OKREŚLENIE DO KTÓREGO MIEJSCA ZAOKRĄGLAMY.
Nie istnieje zaokrąglanie pośrednie: 3,445≈3,45≈3,5≈4 - źle ; 3,445≈3 - dobrze
Szacowanie wyników to szybkie zaokrąglanie, np. 3456+3456≈3500+3500<7000
Kolejność wykonywania działań
Nawiasy/ułamki (zależy co jest pierwsze w działaniu).
Potęgowanie/pierwiastkowanie (zależy co jest pierwsze w działaniu) .
Mnożenie/dzielenie (zależy co jest pierwsze w działaniu).
Dodawanie/odejmowanie (zależy co jest pierwsze w działaniu).